Catégories
Liens
L'intention du projet était de produire une série d'impressions 3D des surfaces disponibles sur la galérie IMAGINARY de Herwig Hauser. Ces surfaces devaient accompagner une exposition au Vieux Port de Marseille, pour que les animateurs puissent s'en saisir et les utiliser dans les explications au public.
En tout, 7 surfaces ont été imprimées à temps pour l'exposition Mathématiques Vivantes et Visuelles, dont quatre sur l'Ultimaker 2 du fablab LFO :
Deux sur la Cubex du Fablab Marseille :
Une sur la MakerBot Replicator du CampusFab à Toulouse :
Les surfaces qui ont été tentées mais ont failli :
Dans la table ci-dessus, toutes les formules implicites proviennent des contributions de Herwig Hauser sur Imaginary.org (galerie Herwig Hauser classic et l'ensemble de surfaces algébriques de l'institut Forwiss), avec éventuellement quelques constantes de rajoutées. Les paramétrisations correspondantes ont été calculées par Alba. L'intérêt d'une paramétrisation explicite pour la construction d'un modèle 3D est que les modèles qui en sortent sont plus propres, car approcher numériquement la solution d'une équation comporte des erreurs beaucoup plus grosses que d'évaluer une fonction. C'est particulièrement vrai dans le cas des équations polynomiales et l'évaluation des polynômes.
| Nom | Équation polynomiale | Paramétrisation(s) | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zitrus | $9(x | 2+z | 2)=64y | 3(1-y) | 3$ | $\left\{\begin{array}{rcl}x&=&\frac83\sin | 3(u)\cos | 3(u)\cos(v)\\y&=&\cos | 2(u)\\z&=&\frac83\sin | 3(u)\cos | 3(u)\sin(v)\end{array}\right.$ | ||||||||||||
| Limão | $x | 2=y | 3z | 3$ | $\left\{\begin{array}{rcl}x&=&u | 3v | 3\\y&=&\pm u | 2\\z&=&\pm v | 2\end{array}\right.$ | ||||||||||||||
| Vis-à-vis | $x | 2+y | 2+y | 4+z | 3=x | 3+z | 4$ | ||||||||||||||||
| Calypso | $x | 2+y | 2z=z | 2$ | $\left\{\begin{array}{rcl}x&=&v | 2\sin(u)&\\y&=&v\cos(u)&\\z&=&v | 2\end{array}\right.$ | $\left\{\begin{array}{rcl}x&=&v | 2\cos(u)&\\y&=&v\sqrt{2\sin(u)}&\\z&=&v | 2(\sin(u)-1)\end{array}\right.$ | |||||||||||||
| Calyx | $x | 2+y | 2z | 3=z | 4$ | $\left\{\begin{array}{rcl}x&=&v | 4\sin(u)&\\y&=&v\cos(u)&\\z&=&v | 2\end{array}\right.$ | $\left\{\begin{array}{rcl}x&=&v | 4\sin(u)(\cos(u)-1)&\\y&=&v\sqrt{2\cos(u)}&\\z&=&v | 2(\cos(u)-1)\end{array}\right.$ | ||||||||||||
| Daisy | $(x | 2-y | 3) | 2=(z | 2-y | 2) | 3$ | $\left\{\begin{array}{rcl}x&=&v | 3(\sin(u)+(\sin | 2(u)-1) (\sin(u)+\cos(u))) | 2\\y&=&v | 2 (\sin(u)+(\sin | 2(u)-1) (\sin(u)+\cos(u))) \sin(u) \\z&=&v | 2(\sin | 3(u)-\cos | 3(u))\end{array}\right.$ | |||||||
| Diabolo | $x | 2=(y | 2+z | 2) | 2$ | $\left\{\begin{array}{rcl}x&=&\pm(u | 2+v | 2)\\y&=&u\\z&=&v\end{array}\right.$ | |||||||||||||||
| Ding Dong | $x | 2+y | 2+z | 2=z | 3$ | $\left\{\begin{array}{rcl}x&=&\frac{v | 6+1}{3\sqrt{3}v | 3}\cos(u)\\y&=&\frac{v | 6+1}{3\sqrt{3}v | 3}\sin(u)\\z&=&\frac{-1+v | 2-v | 4}{3 v | 2}\end{array}\right.$ | $\left\{\begin{array}{rcl}x&=&\frac2{3\sqrt{3}}\cos\left(\frac{3v}2\right)\cos(u)\\y&=&\frac2{3\sqrt{3}}\cos\left(\frac{3v}2\right)\sin(u)\\z&=&\frac{1-2\cos(v)}3\end{array}\right.$ | |||||||||
| Distel | $x | 2+y | 2+z | 2+1500(x | 2+y | 2)(x | 2+z | 2)(y | 2+z | 2)=1$ | $ $ | ||||||||||||
| Dullo | $x | 2+y | 2=(x | 2+y | 2+z | 2) | 2$ | $\left\{\begin{array}{rcl}x&=&\frac{1-cos(v)}2\cos(u)\\y&=&\frac{1-cos(v)}2\sin(u)\\z&=&-\frac12\sin(v)\end{array}\right.$ | |||||||||||||||
| Eistüte | $(x | 2+y | 2) | 3=4x | 2y | 2(z | 2+1)$ | $\left\{\begin{array}{rcl}x&=&\sin(2u)\sin(u)\sqrt{v | 2+1}\\y&=&\sin(2u)\cos(u)\sqrt{v | 2+1}\\z&=&v\end{array}\right.$ | |||||||||||||
| Helix | $6x | 2=2x | 4+y | 2z | 2$ | $\left\{\begin{array}{rcl}x&=&\frac1{\sqrt2}\sqrt{3\pm\sqrt{9\pm4u | 2v | 2}}\\y&=&u\\z&=&v\end{array}\right.$ | $\left\{\begin{array}{rcl}x&=&\sqrt{3}\cos(u)\\y\text{ ou }z&=&\sqrt{3}v\\y\text{ ou }z&=&\sqrt{\frac32}\frac{\sin{2u}}v\end{array}\right.$ | ||||||||||||||
| Herz | $x | 2z | 2+z | 4=y | 2+z | 3$ | $\left\{\begin{array}{rcl}x&=&\frac12v\sin(u)\\y&=&\pm\frac12\sqrt{v | 2-1}(1+v\cos(u))\\z&=&\frac12(1+v\cos(u))\end{array}\right.$ | |||||||||||||||
| Himmel & Hölle | $x | 2=y | 2z | 2$ | $\left\{\begin{array}{rcl}x&=&\pm uv\\y&=&u\\z&=&v\end{array}\right.$ | ||||||||||||||||||
| Kolibri | $x | 2=y | 2z | 2+z | 3$ | $\left\{\begin{array}{rcl}x&=&u(u | 2-v | 2)\\y&=&v\\z&=&u | 2-v | 2\end{array}\right.$ | |||||||||||||
| Kreisel | $60(x | 2+y | 2)z | 4=(60-x | 2-y | 2-z | 2) | 3$ | $\left\{\begin{array}{rcl}x&=&\sqrt{\frac{60}{1+60(v | 3+v | 2)}}\cos(u)\\y&=&\sqrt{\frac{60}{1+60(v | 3+v | 2)}}\sin(u)\\z&=&\pm60\sqrt{\frac{v | 3}{1+60(v | 3+v | 2)}}\end{array}\right.$ | |||||||
| Miau | $x | 2yz+x | 2z | 2+2y | 3z+3y | 3=0$ | $ $ | ||||||||||||||||
| Nepali | $(xy-z | 3-1) | 2=(1-x | 2-y | 2) | 3$ | $\left\{\begin{array}{rcl}x&=&\cos(v)\cos(u)\\y&=&\cos(v)\sin(u)\\z&=&\sqrt[3]{\frac12\cos | 2(v)\sin(2u)-1-\sin | 3(v)}\end{array}\right.$ | ||||||||||||||
| Seepferdchen | $(x | 2-y | 3) | 2=(x+y | 2)z | 3$ | $ $ | ||||||||||||||||
| Solitude | $x | 2yz+xy | 2+y | 3+y | 3z=x | 2z | 2$ | $ $ | |||||||||||||||
| Tanz | $2x | 4=x | 2+y | 2z | 2$ | $\left\{\begin{array}{rcl}x&=&\pm\frac12\sqrt{1+\sqrt{1+2u | 2v | 2}}\\y&=&\frac1{\sqrt{2}}u\\z&=&\frac1{\sqrt{2}}v\end{array}\right.$ | |||||||||||||||
| Taube | $256z | 3 − 128x | 2z | 2+16x | 4z+144xy | 2z−4x | 3y | 2−27y | 4=0$ | $\left\{\begin{array}{rcl}x&=&3(u | 2-v | 2)\\y&=&\pm2v(3u | 2-v | 2)\\z&=&3u | 2v | 2\end{array}\right.$ | $\left\{\begin{array}{rcl}x&=&-3(u | 2+v | 2)\\y&=&\pm2v(3u | 2+v | 2)\\z&=&-3u | 2v | 2\end{array}\right.$ |
| Tülle | $yz\cdot (x | 2+y-z)=0$ | $\left\{\begin{array}{rcl}x&=&u\\y&=&v\\z&=&u | 2+v\end{array}\right.$ | $\left\{\begin{array}{rcl}x&=&u\\y\text{ ou }z&=&v\\y\text{ ou }z&=&0\end{array}\right.$ | ||||||||||||||||||
| Zeck | $x | 2+y | 2=z | 3\cdot(1-z)$ | $\left\{\begin{array}{rcl}x&=&\sin(v)\cos | 3(v)\cos(u)\\y&=&\sin(v)\cos | 3(v)\sin(u)\\z&=&\cos | 2(v)\end{array}\right.$ | |||||||||||||||
| Spitz | $(y | 2-x | 2-z | 2) | 3=27x | 2y | 3z | 2$ | $\left\{\begin{array}{rcl}x&=&4v | 3\cos(u)\\y&=&6v | 2\sqrt[3]{\sin | 2(2u)}-\sqrt{4v | 2\sqrt[3]{sin(2u) | 4}+16v | 6}\\z&=&4v | 3\sin(u)\end{array}\right.$ | |||||||
| Schneeflocke | $x | 3+y | 2z | 3+yz | 4=0$ | $\left\{\begin{array}{rcl}x&=&\pm(u-v)\sqrt[3]{uv}\\y&=&u\\z&=&v-u\end{array}\right.$ |
Ci-dessus, un script pour MathMod contenant toutes les surfaces listées dans la section Formules de ce wiki, ainsi qu'une paramétrisation pour la plupart d'entre elles.
{ "MathModels": [ { "Iso3D": { "Component": [ "Zitrus" ], "Fxyz": [ "9*(x^2+z^2)-64*y^3*(1-y)^3" ], "Name": [ "Zitrus" ], "Xmax": [ "1/3" ], "Xmin": [ "-1/3" ], "Ymax": [ "1" ], "Ymin": [ "0" ], "Zmax": [ "1/3" ], "Zmin": [ "-1/3" ] } }, { "Param3D": { "Component": [ "Zitrus P" ], "Description": [ "Parametric Zitrus" ], "Fx": [ "(8/3)*sin(u)^3*cos(u)^3*cos(v)" ], "Fy": [ "cos(u)^2" ], "Fz": [ "(8/3)*sin(u)^3*cos(u)^3*sin(v)" ], "Name": [ "Zitrus P" ], "Umax": [ "pi/2" ], "Umin": [ "0" ], "Vmax": [ "2*pi" ], "Vmin": [ "0" ] } }, { "Iso3D": { "Component": [ "Limão" ], "Fxyz": [ "x^2-y^3*z^3" ], "Name": [ "Limão" ], "Xmax": [ "1" ], "Xmin": [ "-1" ], "Ymax": [ "1" ], "Ymin": [ "-1" ], "Zmax": [ "1" ], "Zmin": [ "-1" ] } }, { "Param3D": { "Component": ["Limão_+","Limão_-"], "Description": ["Parametric Limão"], "Fx": ["u^3*v^3","u^3*v^3"], "Fy": ["v^2","-v^2"], "Fz": ["u^2","-u^2"], "Name": ["Limão P"], "Umax": ["1","1"], "Umin": ["-1","-1"], "Vmax": ["1","1"], "Vmin": ["-1","-1"] } }, { "Iso3D": { "Component": [ "Vis-à-vis" ], "Fxyz": [ "x^2-x^3+y^2+y^4+z^3-z^4" ], "Name": [ "Vis-à-vis" ], "Xmax": [ "1.73" ], "Xmin": [ "-1.73" ], "Ymax": [ "2" ], "Ymin": [ "-2" ], "Zmax": [ "1.65" ], "Zmin": [ "-1.65" ] } }, { "Iso3D": { "Component": [ "Calypso" ], "Fxyz": [ "x^2+y^2*z-z^2" ], "Name": [ "Calypso" ], "Xmax": [ "2.55" ], "Xmin": [ "-2.55" ], "Ymax": [ "2.55" ], "Ymin": [ "-2.55" ], "Zmax": [ "2.55" ], "Zmin": [ "-2.55" ] } }, { "Param3D": { "Component": [ "CalypsoPolar_+", "CalypsoPolar_-" ], "Description": [ "Calypso parametrized polar" ], "Fx": [ "v^2*sin(u)", "v^2*cos(u)" ], "Fy": [ "v*cos(u)", "v*sqrt(2*sin(u))" ], "Fz": [ "v^2", "v^2*(sin(u)-1)" ], "Name": [ "Calypso polar" ], "Umax": [ "2*pi", "pi" ], "Umin": [ "0", "0" ], "Vmax": [ "1", "1" ], "Vmin": [ "0", "-1" ] } }, { "Iso3D": { "Component": [ "Calyx" ], "Fxyz": [ "x^2+y^2*z^3-z^4" ], "Name": [ "Calyx" ], "Xmax": [ "4" ], "Xmin": [ "-4" ], "Ymax": [ "2" ], "Ymin": [ "-2" ], "Zmax": [ "2" ], "Zmin": [ "-2" ] } }, { "Param3D": { "Component": [ "CalyxPolar_+", "CalyxPolar_-" ], "Description": [ "Calyx parametrized polar" ], "Fx": [ "v^4*sin(u)", "v^4*sin(u)*(cos(u)-1)" ], "Fy": [ "v*cos(u)", "v*sqrt(2*cos(u))" ], "Fz": [ "v^2", "v^2*(cos(u)-1)" ], "Name": [ "Calyx polar" ], "Umax": [ "2*pi", "pi/2" ], "Umin": [ "0", "-pi/2" ], "Vmax": [ "1", "1" ], "Vmin": [ "0", "-1" ] } }, { "Iso3D": { "Component": [ "Daisy" ], "Fxyz": [ "(x^2-y^3)^2-(z^2-y^2)^3" ], "Name": [ "Daisy" ], "Xmax": [ "0.1" ], "Xmin": [ "-0.1" ], "Ymax": [ "0.21" ], "Ymin": [ "-0.15" ], "Zmax": [ "0.21" ], "Zmin": [ "-0.21" ] } }, { "Param3D": { "Description": ["Parametric Daisy"], "Name": ["Daisy P"], "Component": ["Daisy_++","Daisy_+-","Daisy_-+","Daisy_--"], "Fx": ["sqrt((v+u)^3-u^3)","sqrt((v-u)^3+u^3)","-sqrt((v-u)^3+u^3)","-sqrt((v+u)^3-u^3)"], "Fy": ["-u","u","u","-u"], "Fz": ["sqrt((v+u)^2+u^2)","-sqrt((v-u)^2+u^2)","sqrt((v-u)^2+u^2)","-sqrt((v+u)^2+u^2)"], "Umax": [ "1", "1", "1", "1"], "Umin": ["-1","-1","-1","-1"], "Vmax": [ "1", "1", "1", "1"], "Vmin": [ "0", "0", "0", "0"] } }, { "Iso3D": { "Component": [ "Diabolo" ], "Fxyz": [ "x^2-(y^2+z^2)^2" ], "Name": [ "Diabolo" ], "Xmax": [ "1" ], "Xmin": [ "-1" ], "Ymax": [ "1" ], "Ymin": [ "-1" ], "Zmax": [ "1" ], "Zmin": [ "-1" ] } }, { "Param3D": { "Component": [ "DiaboloP_+","DiaboloP_-" ], "Description": [ "Parametric diabolo" ], "Fx": [ "u^2","-u^2" ], "Fy": [ "u*cos(v)","u*cos(v)" ], "Fz": [ "u*sin(v)","u*sin(v)" ], "Name": [ "Diabolo P" ], "Umax": [ "pi/2","0" ], "Umin": [ "0","-pi/2" ], "Vmax": [ "2*pi","2*pi" ], "Vmin": [ "0","0" ] } }, { "Iso3D": { "Component": [ "Ding Dong" ], "Fxyz": [ "x^2+y^2+z^3-z^2" ], "Name": [ "Ding Dong" ], "Xmax": [ "1.34" ], "Xmin": [ "-1.34" ], "Ymax": [ "1.34" ], "Ymin": [ "-1.34" ], "Zmax": [ "1" ], "Zmin": [ "-0.85" ] } }, { "Param3D": { "Component": [ "DingDongP_+", "DingDongP_-" ], "Description": [ "Parametric ding dong" ], "Fx": [ "2/(3*sqrt(3))*sin(3*v/2)*cos(u)", "-(v^6+1)/(3*sqrt(3)*v^3)*cos(u)" ], "Fy": [ "2/(3*sqrt(3))*sin(3*v/2)*sin(u)", "-(v^6+1)/(3*sqrt(3)*v^3)*sin(u)" ], "Fz": [ "(1+2*cos(v))/3", "-(1-v^2+v^4)/(3*v^2)" ], "Name": [ "Ding Dong P" ], "Umax": [ "2*pi", "2*pi" ], "Umin": [ "0", "0" ], "Vmax": [ "pi", "1.7" ], "Vmin": [ "0", "1"] } }, { "Iso3D": { "Component": [ "Distel" ], "Fxyz": [ "x^2+y^2+z^2+1500*(x^2+y^2)*(x^2+z^2)*(y^2+z^2)-1" ], "Name": [ "Distel" ], "Xmax": [ "1" ], "Xmin": [ "-1" ], "Ymax": [ "1" ], "Ymin": [ "-1" ], "Zmax": [ "1" ], "Zmin": [ "-1" ] } }, { "Iso3D": { "Component": [ "Dullo" ], "Fxyz": [ "(x^2+y^2+z^2)^2-(x^2+y^2)" ], "Name": [ "Dullo" ], "Xmax": [ "1" ], "Xmin": [ "-1" ], "Ymax": [ "1" ], "Ymin": [ "-1" ], "Zmax": [ "0.5" ], "Zmin": [ "-0.5" ] } }, { "Param3D": { "Component": [ "Dullo P" ], "Description": [ "Parametric dullo" ], "Fx": [ "(1-cos(u))*cos(v)/2" ], "Fy": [ "(1-cos(u))*sin(v)/2" ], "Fz": [ "-sin(u)/2" ], "Name": [ "Dullo P" ], "Umax": [ "2*pi" ], "Umin": [ "0" ], "Vmax": [ "2*pi" ], "Vmin": [ "0" ] } }, { "Iso3D": { "Component": [ "Eistüte" ], "Fxyz": [ "(x^2+y^2)^3-4*x^2*y^2*(z^2+1)" ], "Name": [ "Eistüte" ], "Xmax": [ "10" ], "Xmin": [ "-10" ], "Ymax": [ "10" ], "Ymin": [ "-10" ], "Zmax": [ "10" ], "Zmin": [ "-10" ] } }, { "Param3D": { "Component": [ "Eistüte P" ], "Description": [ "Parametric Eistüte" ], "Fx": [ "sin(2*u)*sin(u)*sqrt(v^2+1)" ], "Fy": [ "sin(2*u)*cos(u)*sqrt(v^2+1)" ], "Fz": [ "v" ], "Name": [ "Eistüte P" ], "Umax": [ "2*pi" ], "Umin": [ "0" ], "Vmax": [ "10" ], "Vmin": [ "-10" ] } }, { "Iso3D": { "Component": [ "Helix" ], "Fxyz": [ "2*x^4+y^2*z^2-6*x^2" ], "Name": [ "Helix" ], "Xmax": [ "sqrt(3)" ], "Xmin": [ "-sqrt(3)" ], "Ymax": [ "3*sqrt(1.5)" ], "Ymin": [ "-3*sqrt(1.5)" ], "Zmax": [ "3*sqrt(1.5)" ], "Zmin": [ "-3*sqrt(1.5)" ] } }, { "Param3D": { "Component": [ "Helix_X++", "Helix_X+-", "Helix_X-+", "Helix_X--", "Helix_Y++", "Helix_Y+-", "Helix_Y-+", "Helix_Y--", "Helix_Z++", "Helix_Z+-", "Helix_Z-+", "Helix_Z--" ], "Description": [ "Parametric Helix" ], "Fx": [ "sqrt(1.5+sqrt(2.25-u^2*v^2))", "sqrt(1.5-sqrt(2.25-u^2*v^2))", "-sqrt(1.5+sqrt(2.25-u^2*v^2))", "-sqrt(1.5-sqrt(2.25-u^2*v^2))", "sqrt(1.5*(1+cos(u)))", "sqrt(1.5*(1+sin(u)))", "-sqrt(1.5*(1+sin(u)))", "-sqrt(1.5*(1+cos(u)))", "sqrt(1.5*(1+sin(u)))", "sqrt(1.5*(1+cos(u)))", "-sqrt(1.5*(1+cos(u)))", "-sqrt(1.5*(1+sin(u)))" ], "Fy": [ "v", "u", "u", "v", "sqrt(1.5)*v", "sqrt(1.5)*v", "sqrt(1.5)*v", "sqrt(1.5)*v", "sqrt(1.5)*cos(u)/v", "sqrt(1.5)*sin(u)/v", "sqrt(1.5)*sin(u)/v", "sqrt(1.5)*cos(u)/v" ], "Fz": [ "u", "v", "v", "u", "sqrt(1.5)*sin(u)/v", "sqrt(1.5)*cos(u)/v", "sqrt(1.5)*cos(u)/v", "sqrt(1.5)*sin(u)/v", "sqrt(1.5)*v", "sqrt(1.5)*v", "sqrt(1.5)*v", "sqrt(1.5)*v" ], "Name": [ "Helix P" ], "Umax": [ "sqrt(1.5)", "sqrt(1.5)", "sqrt(1.5)", "sqrt(1.5)", "2*pi", "2*pi", "2*pi", "2*pi", "2*pi", "2*pi", "2*pi", "2*pi" ], "Umin": [ "-sqrt(1.5)", "-sqrt(1.5)", "-sqrt(1.5)", "-sqrt(1.5)", "0", "0", "0", "0", "0", "0", "0", "0" ], "Vmax": [ "sqrt(1.5)", "sqrt(1.5)", "sqrt(1.5)", "sqrt(1.5)", "3", "-1", "3", "-1", "3", "-1", "3", "-1" ], "Vmin": [ "-sqrt(1.5)", "-sqrt(1.5)", "-sqrt(1.5)", "-sqrt(1.5)", "1", "-3", "1", "-3", "1", "-3", "1", "-3" ] } }, { "Iso3D": { "Component": [ "Herz" ], "Fxyz": [ "x^2*z^2+z^4-y^2-z^3" ], "Name": [ "Herz" ], "Xmax": [ "3" ], "Xmin": [ "-3" ], "Ymax": [ "2.7" ], "Ymin": [ "-2.7" ], "Zmax": [ "3.5" ], "Zmin": [ "-2.5" ] } }, { "Param3D": { "Component": [ "HerzPolar_+", "HerzPolar_-" ], "Description": [ "Herz parametrized polar" ], "Fx": [ "0.5*v*sin(u)", "0.5*v*cos(u)" ], "Fy": [ "0.5*sqrt(v^2-1)*(1+v*cos(u))", "-0.5*sqrt(v^2-1)*(1+v*sin(u))" ], "Fz": [ "0.5*(1+v*cos(u))", "0.5*(1+v*sin(u))" ], "Name": [ "Herz polar" ], "Umax": [ "2*pi", "2*pi" ], "Umin": [ "0", "0" ], "Vmax": [ "2", "2" ], "Vmin": [ "1", "1" ] } }, { "Iso3D": { "Component": [ "HimmelHolle_01", "HimmelHolle_02" ], "Fxyz": [ "x-y*z", "x+y*z" ], "Name": [ "Himmel & Hölle" ], "Xmax": [ "1", "1" ], "Xmin": [ "-1", "-1" ], "Ymax": [ "1", "1" ], "Ymin": [ "-1", "-1" ], "Zmax": [ "1", "1" ], "Zmin": [ "-1", "-1" ] } }, { "Param3D": { "Component": [ "HimmerHolleP_01", "HimmerHolleP_02" ], "Description": [ "parametric Himmer & Hölle" ], "Fx": [ "u*v", "-u*v" ], "Fy": [ "u", "u" ], "Fz": [ "v", "v" ], "Name": [ "Himmer & Hölle P" ], "Umax": [ "1.2", "1.2" ], "Umin": [ "-1.2", "-1.2" ], "Vmax": [ "1.2", "1.2" ], "Vmin": [ "-1.2", "-1.2" ] } }, { "Iso3D": { "Component": [ "Kolibri" ], "Fxyz": [ "y^2*z^2+z^3-x^2" ], "Name": [ "Kolibri" ], "Xmax": [ "1" ], "Xmin": [ "-1" ], "Ymax": [ "1" ], "Ymin": [ "-1" ], "Zmax": [ "1" ], "Zmin": [ "-1" ] } }, { "Param3D": { "Component": [ "KolibriP" ], "Description": [ "parametrized Kolibri" ], "Fx": [ "u*(u^2-v^2)" ], "Fy": [ "v" ], "Fz": [ "u^2-v^2" ], "Name": [ "Kolibri P" ], "Umax": [ "1" ], "Umin": [ "-1" ], "Vmax": [ "1" ], "Vmin": [ "-1" ] } }, { "Iso3D": { "Component": [ "Kreisel" ], "Fxyz": [ "(60-x^2-y^2-z^2)^3-60*(x^2+y^2)*z^4" ], "Name": [ "Kreisel" ], "Xmax": [ "sqrt(60)" ], "Xmin": [ "-sqrt(60)" ], "Ymax": [ "sqrt(60)" ], "Ymin": [ "-sqrt(60)" ], "Zmax": [ "sqrt(60)" ], "Zmin": [ "-sqrt(60)" ] } }, { "Param3D": { "Component": [ "Kreisel_03", "Kreisel_04", "Kreisel_02", "Kreisel_01" ], "Description": [ "Kreisel parametrized polar" ], "Fx": [ "sqrt(60/(1+60*(-v^3+v^2)))*cos(u)", "sqrt(60/(1+60*(v^3+v^2)))*cos(u)", "sqrt(-60*v^3/(-v^3+60*(1-v)))*cos(u)", "sqrt(60*v^3/(v^3+60*(1+v)))*cos(u)" ], "Fy": [ "sqrt(60/(1+60*(-v^3+v^2)))*sin(u)", "sqrt(60/(1+60*(v^3+v^2)))*sin(u)", "sqrt(-60*v^3/(-v^3+60*(1-v)))*sin(u)", "sqrt(60*v^3/(v^3+60*(1+v)))*sin(u)" ], "Fz": [ "60*sqrt(-v^3/(1+60*(v^2-v^3)))", "-60*sqrt(v^3/(1+60*(v^3+v^2)))", "-60/sqrt(-v^3+60*(1-v))", "60/sqrt(v^3+60*(1+v))" ], "Name": [ "Kreisel polar" ], "Umax": [ "2*pi", "2*pi", "2*pi", "2*pi" ], "Umin": [ "0", "0", "0", "0" ], "Vmax": [ "0", "0.25", "0", "4" ], "Vmin": [ "-0.25", "0", "-4", "0" ] } },{ "Iso3D": { "Component": [ "Miau" ], "Fxyz": [ "x^2*y*z+x^2*z^2+2*y^3*z+3*y^3" ], "Name": [ "Miau" ], "Xmax": [ "5" ], "Xmin": [ "-5" ], "Ymax": [ "5" ], "Ymin": [ "-5" ], "Zmax": [ "5" ], "Zmin": [ "-5" ] } }, { "Iso3D": { "Component": [ "Nepali" ], "Fxyz": [ "(x*y-z^3-1)^2-(1-x^2-y^2)^3" ], "Name": [ "Nepali" ], "Xmax": [ "1" ], "Xmin": [ "-1" ], "Ymax": [ "1" ], "Ymin": [ "-1" ], "Zmax": [ "0" ], "Zmin": [ "-1.26" ] } }, { "Param3D": { "Component": [ "Nepali Polar" ], "Description": [ "Nepali parametrized polar" ], "Fx": [ "sin(v)*cos(u)" ], "Fy": [ "sin(v)*sin(u)" ], "Fz": [ "-(-(sin(v)^2*sin(2*u)/2-1+cos(v)^3))^(1/3)" ], "Name": [ "Nepali polar" ], "Umax": [ "2*pi" ], "Umin": [ "0" ], "Vmax": [ "pi" ], "Vmin": [ "0" ] } }, { "Iso3D": { "Component": [ "Seepferdchen" ], "Fxyz": [ "(x^2-y^3)^2-(x+y^2)*z^3" ], "Name": [ "Seepferdchen" ], "Xmax": [ "25" ], "Xmin": [ "-25" ], "Ymax": [ "15" ], "Ymin": [ "-15" ], "Zmax": [ "25" ], "Zmin": [ "-25" ] } }, { "Iso3D": { "Component": [ "Solitude" ], "Fxyz": [ "x^2*y*z+x*y^2+y^3+y^3*z-x^2*z^2" ], "Name": [ "Solitude" ], "Xmax": [ "25" ], "Xmin": [ "-25" ], "Ymax": [ "25" ], "Ymin": [ "-25" ], "Zmax": [ "25" ], "Zmin": [ "-25" ] } }, { "Iso3D": { "Component": [ "Tanz" ], "Fxyz": [ "2*x^4-x^2-y^2*z^2" ], "Name": [ "Tanz" ], "Xmax": [ "25" ], "Xmin": [ "-25" ], "Ymax": [ "25" ], "Ymin": [ "-25" ], "Zmax": [ "25" ], "Zmin": [ "-25" ] } }, { "Param3D": { "Component": [ "TanzP_+", "TanzP_-" ], "Description": [ "parametrized Tanz" ], "Fx": [ "sqrt(1+sqrt(1+2*u^2*v^2))/2", "-sqrt(1+sqrt(1+2*u^2*v^2))/2" ], "Fy": [ "u/sqrt(2)", "u/sqrt(2)" ], "Fz": [ "v/sqrt(2)", "v/sqrt(2)" ], "Name": [ "Tanz P" ], "Umax": [ "25", "25" ], "Umin": [ "-25", "-25" ], "Vmax": [ "25", "25" ], "Vmin": [ "-25", "-25" ] } }, { "Iso3D": { "Component": [ "Taube" ], "Fxyz": [ "256*z^3-128*x^2*z^2+16*x^4*z+144*x*y^2*z-4*x^3*y^2-27*y^4" ], "Name": [ "Taube" ], "Xmax": [ "25" ], "Xmin": [ "-25" ], "Ymax": [ "25" ], "Ymin": [ "-25" ], "Zmax": [ "25" ], "Zmin": [ "-25" ] } }, { "Param3D": { "Component": [ "TaubePs_1", "TaubePs_2", "TaubePs_3", "TaubePs_4" ], "Description": [ "Parametric Taube" ], "Fx": [ "3*(u^2-v^2)", "-3*(u^2+v^2)", "-3*(u^2+v^2)", "3*(v^2-u^2)" ], "Fy": [ "2*v*(3*u^2-v^2)", "-2*v*(3*u^2+v^2)", "2*u*(3*v^2+u^2)", "-2*u*(3*v^2-u^2)" ], "Fz": [ "3*u^2*v^2", "-3*u^2*v^2", "-3*u^2*v^2", "3*u^2*v^2" ], "Name": [ "Taube Ps" ], "Umax": [ "2", "2", "2", "2" ], "Umin": [ "0", "0", "0", "0" ], "Vmax": [ "2", "2", "2", "2" ], "Vmin": [ "0", "0", "0", "0" ] } }, { "Iso3D": { "Component": [ "Tulle_01", "Tulle_02", "Tulle_03" ], "Fxyz": [ "x^2+y-z", "y", "z" ], "Name": [ "Tulle" ], "Xmax": [ "2", "2", "2" ], "Xmin": [ "-2", "-2", "-2" ], "Ymax": [ "2", "2", "2" ], "Ymin": [ "-2", "-2", "-2" ], "Zmax": [ "2", "2", "2" ], "Zmin": [ "-2", "-2", "-2" ] } }, { "Param3D": { "Component": [ "TulleP_01", "TulleP_02", "TulleP_03" ], "Description": [ "parametrized Tulle" ], "Fx": [ "v", "u", "u" ], "Fy": [ "0.5*(u-v^2)", "0", "v" ], "Fz": [ "0.5*(u+v^2)", "v", "0" ], "Name": [ "Tulle P" ], "Umax": [ "1", "1", "1" ], "Umin": [ "-1", "-1", "-1" ], "Vmax": [ "1", "1", "1" ], "Vmin": [ "-1", "-1", "-1" ] } }, { "Iso3D": { "Component": [ "Zeek" ], "Fxyz": [ "x^2+y^2-z^3*(1-z)" ], "Name": [ "Zeek" ], "Xmax": [ "0.1875*sqrt(3)" ], "Xmin": [ "-0.1875*sqrt(3)" ], "Ymax": [ "0.1875*sqrt(3)" ], "Ymin": [ "-0.1875*sqrt(3)" ], "Zmax": [ "1" ], "Zmin": [ "0" ] } }, { "Param3D": { "Component": [ "Zeek Polar" ], "Description": [ "Parametric Zeek" ], "Fx": [ "sin(v)*cos(v)^3*cos(u)" ], "Fy": [ "sin(v)*cos(v)^3*sin(u)" ], "Fz": [ "cos(v)^2" ], "Name": [ "Zeek Polar" ], "Umax": [ "pi/2" ], "Umin": [ "-pi/2" ], "Vmax": [ "pi/2" ], "Vmin": [ "-pi/2" ] } }, { "Iso3D": { "Component": [ "Spitz" ], "Fxyz": [ "(y^2-x^2-z^2)^3-27*x^2*y^3*z^2" ], "Name": [ "Spitz" ], "Xmax": [ "2" ], "Xmin": [ "-2" ], "Ymax": [ "2" ], "Ymin": [ "-2" ], "Zmax": [ "2" ], "Zmin": [ "-2" ] } }, { "Param3D": { "Component": [ "SpitzPolar_+", "SpitzPolar_-" ], "Description": [ "Parametric Spitz" ], "Fx": [ "4*v^3*cos(u)", "4*v^3*cos(u)" ], "Fy": [ "6*v^2*(sin(2*u)^2)^(1/3)+sqrt(4*v^2*(sin(2*u)^4)^(1/3)+16*v^6)", "6*v^2*(sin(2*u)^2)^(1/3)-sqrt(4*v^2*(sin(2*u)^4)^(1/3)+16*v^6)" ], "Fz": [ "4*v^3*sin(u)", "4*v^3*sin(u)" ], "Name": [ "Spitz Polar" ], "Umax": [ "2*pi", "2*pi" ], "Umin": [ "0", "0" ], "Vmax": [ "1.5874", "1.5874" ], "Vmin": [ "0", "0" ] } }, { "Iso3D": { "Component": [ "Schneeflocke" ], "Fxyz": [ "x^3+y^2*z^3+y*z^4" ], "Name": [ "Schneeflocke" ], "Xmax": [ "1" ], "Xmin": [ "-1" ], "Ymax": [ "1" ], "Ymin": [ "-1" ], "Zmax": [ "1" ], "Zmin": [ "-1" ] } }, { "Param3D": { "Component": [ "SchneeflockePX_1", "SchneeflockePX_2", "SchneeflockePX_3", "SchneeflockePX_4" ], "Description": [ "Parametric Schneeflocke" ], "Fx": [ "(u-v)*(u*v)^(1/3)", "-(u-v)*(-u*v)^(1/3)", "(u-v)*(u*v)^(1/3)", "-(u-v)*(-u*v)^(1/3)" ], "Fy": [ "u", "u", "u", "u" ], "Fz": [ "v-u", "v-u", "v-u", "v-u" ], "Name": [ "Schneeflocke P X" ], "Umax": [ "2", "0", "0", "2" ], "Umin": [ "0", "-2", "-2", "0" ], "Vmax": [ "2", "2", "0", "0" ], "Vmin": [ "0", "0", "-2", "-2" ] } } ] }
Voici un script pour MathMod contenant les surface accompagnées ou bien d'une sphère avec laquelle les intersecter, ou bien d'une sphère les contenant.
{ "MathModels": [ { "Param3D": { "Component": [ "Zitrus P", "Sphere" ], "Description": [ "Parametric Zitrus with sphere" ], "Fx": [ "(8/3)*sin(u)^3*cos(u)^3*cos(v)", "1/2*cos(v)*cos(u)" ], "Fy": [ "cos(u)^2", "1/2*cos(v)*sin(u)+1/2" ], "Fz": [ "(8/3)*sin(u)^3*cos(u)^3*sin(v)", "1/2*sin(v)" ], "Name": [ "Zitrus⊂Sphere½" ], "Umax": [ "pi/2", "2*pi" ], "Umin": [ "0", "0" ], "Vmax": [ "2*pi", "pi/2" ], "Vmin": [ "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "Limão_+", "Limão_-", "Sphere" ], "Description": [ "Parametric Limão" ], "Fx": [ "u^3*v^3", "u^3*v^3", "cos(v)*cos(u)" ], "Fy": [ "v^2", "-v^2", "cos(v)*sin(u)" ], "Fz": [ "u^2", "-u^2", "sin(v)" ], "Name": [ "Limão+Sphere1" ], "Umax": [ "1", "1", "2*pi" ], "Umin": [ "-1", "-1", "0" ], "Vmax": [ "1", "1", "pi/2" ], "Vmin": [ "-1", "-1", "-pi/2" ] } }, { "Param3D": { "Component": [ "CalypsoPolar_+", "CalypsoPolar_-", "Sphere" ], "Description": [ "Calypso parametrized polar" ], "Fx": [ "v^2*sin(u)", "v^2*cos(u)", "sqrt(2)*cos(v)*cos(u)" ], "Fy": [ "v*cos(u)", "v*sqrt(2*sin(u))", "sqrt(2)*cos(v)*sin(u)" ], "Fz": [ "v^2", "v^2*(sin(u)-1)", "sqrt(2)*sin(v)" ], "Name": [ "Calypso+Sphere√2" ], "Umax": [ "2*pi", "pi", "2*pi" ], "Umin": [ "0", "0", "0" ], "Vmax": [ "1", "1", "pi/2" ], "Vmin": [ "0", "-1", "-pi/2" ] } }, { "Param3D": { "Component": [ "CalyxPolar_+", "CalyxPolar_-", "Sphere" ], "Description": [ "Calyx parametrized polar" ], "Fx": [ "v^4*sin(u)", "v^4*sin(u)*(cos(u)-1)", "sqrt(2)*cos(v)*cos(u)" ], "Fy": [ "v*cos(u)", "v*sqrt(2*cos(u))", "sqrt(2)*cos(v)*sin(u)" ], "Fz": [ "v^2", "v^2*(cos(u)-1)", "sqrt(2)*sin(v)" ], "Name": [ "Calyx+Sphere√2" ], "Umax": [ "2*pi", "pi/2", "2*pi" ], "Umin": [ "0", "-pi/2", "0" ], "Vmax": [ "1", "1.121", "pi/2" ], "Vmin": [ "0", "-1.121", "-pi/2" ] } }, { "Param3D": { "Component": [ "Daisy_++", "Daisy_+-", "Daisy_-+", "Daisy_--", "Sphere" ], "Description": [ "Parametric Daisy" ], "Fx": [ "sqrt((v+u)^3-u^3)", "sqrt((v-u)^3+u^3)", "-sqrt((v-u)^3+u^3)", "-sqrt((v+u)^3-u^3)", "cos(v)*sin(u)" ], "Fy": [ "-u", "u", "u", "-u", "cos(v)*cos(u)" ], "Fz": [ "sqrt((v+u)^2+u^2)", "-sqrt((v-u)^2+u^2)", "sqrt((v-u)^2+u^2)", "-sqrt((v+u)^2+u^2)", "sin(v)" ], "Name": [ "Daisy + Sphere 1" ], "Umax": [ "1/sqrt(3)", "1/2*(sqrt(5)-1)", "1/2*(sqrt(5)-1)", "1/sqrt(3)", "2*pi" ], "Umin": [ "1/2*(1-sqrt(5))", "-1/sqrt(3)", "-1/sqrt(3)", "1/2*(1-sqrt(5))", "0" ], "Vmax": [ "1.01881", "1.0181", "1.0181", "1.0181", "pi/2" ], "Vmin": [ "0", "0", "0", "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "DiaboloP_+", "DiaboloP_-", "Sphere" ], "Description": [ "Parametric diabolo" ], "Fx": [ "u^2", "-u^2", "sqrt(2)*cos(v)*cos(u)" ], "Fy": [ "u*cos(v)", "u*cos(v)", "sqrt(2)*cos(v)*sin(u)" ], "Fz": [ "u*sin(v)", "u*sin(v)", "sqrt(2)*sin(v)" ], "Name": [ "Diabolo+Sphere√2" ], "Umax": [ "1", "0", "2*pi" ], "Umin": [ "0", "-1", "0" ], "Vmax": [ "2*pi", "2*pi", "pi/2" ], "Vmin": [ "0", "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "DingDongP_+", "DingDongP_-", "Sphere" ], "Description": [ "Parametric ding dong" ], "Fx": [ "2/(3*sqrt(3))*sin(3*v/2)*cos(u)", "-(v^6+1)/(3*sqrt(3)*v^3)*cos(u)", "cos(v)*cos(u)" ], "Fy": [ "2/(3*sqrt(3))*sin(3*v/2)*sin(u)", "-(v^6+1)/(3*sqrt(3)*v^3)*sin(u)", "cos(v)*sin(u)" ], "Fz": [ "(1+2*cos(v))/3", "-(1-v^2+v^4)/(3*v^2)", "sin(v)" ], "Name": [ "Ding Dong + Sphere1" ], "Umax": [ "2*pi", "2*pi", "2*pi" ], "Umin": [ "0", "0", "0" ], "Vmax": [ "pi", "1.564", "pi/2" ], "Vmin": [ "0", "1", "-pi/2" ] } }, { "Param3D": { "Component": [ "Dullo P", "Sphere" ], "Description": [ "Parametric dullo" ], "Fx": [ "(1-cos(u))*cos(v)/2", "cos(v)*cos(u)" ], "Fy": [ "(1-cos(u))*sin(v)/2", "cos(v)*sin(u)" ], "Fz": [ "-sin(u)/2", "sin(v)" ], "Name": [ "Dullo⊂Sphere1" ], "Umax": [ "2*pi", "2*pi" ], "Umin": [ "0", "0" ], "Vmax": [ "2*pi", "pi/2" ], "Vmin": [ "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "Eistüte P", "Sphere" ], "Description": [ "Parametric Eistüte" ], "Fx": [ "sin(2*u)*sin(u)*cosh(v)", "sinh(3)*cos(v)*cos(u)" ], "Fy": [ "sin(2*u)*cos(u)*cosh(v)", "sinh(3)*cos(v)*sin(u)" ], "Fz": [ "sinh(v)", "sinh(3)*sin(v)" ], "Name": [ "Eistüte+SphereSH3" ], "Umax": [ "2*pi", "2*pi" ], "Umin": [ "0", "0" ], "Vmax": [ "3", "pi/2" ], "Vmin": [ "-3", "-pi/2" ] } }, { "Param3D": { "Component": [ "Helix_X++", "Helix_X+-", "Helix_X-+", "Helix_X--", "Helix_Y++", "Helix_Y+-", "Helix_Y-+", "Helix_Y--", "Helix_Z++", "Helix_Z+-", "Helix_Z-+", "Helix_Z--", "Sphere" ], "Description": [ "Parametric Helix" ], "Fx": [ "sqrt(1.5+sqrt(2.25-u^2*v^2))", "sqrt(1.5-sqrt(2.25-u^2*v^2))", "-sqrt(1.5+sqrt(2.25-u^2*v^2))", "-sqrt(1.5-sqrt(2.25-u^2*v^2))", "sqrt(1.5*(1+cos(u)))", "sqrt(1.5*(1+sin(u)))", "-sqrt(1.5*(1+sin(u)))", "-sqrt(1.5*(1+cos(u)))", "sqrt(1.5*(1+sin(u)))", "sqrt(1.5*(1+cos(u)))", "-sqrt(1.5*(1+cos(u)))", "-sqrt(1.5*(1+sin(u)))", "3*sqrt(1.5)*cos(v)*cos(u)" ], "Fy": [ "v", "u", "u", "v", "sqrt(1.5)*v", "sqrt(1.5)*v", "sqrt(1.5)*v", "sqrt(1.5)*v", "sqrt(1.5)*cos(u)/v", "sqrt(1.5)*sin(u)/v", "sqrt(1.5)*sin(u)/v", "sqrt(1.5)*cos(u)/v", "3*sqrt(1.5)*cos(v)*sin(u)" ], "Fz": [ "u", "v", "v", "u", "sqrt(1.5)*sin(u)/v", "sqrt(1.5)*cos(u)/v", "sqrt(1.5)*cos(u)/v", "sqrt(1.5)*sin(u)/v", "sqrt(1.5)*v", "sqrt(1.5)*v", "sqrt(1.5)*v", "sqrt(1.5)*v", "3*sqrt(1.5)*sin(v)" ], "Name": [ "Helix + Sphere3" ], "Umax": [ "sqrt(1.5)", "sqrt(1.5)", "sqrt(1.5)", "sqrt(1.5)", "2*pi", "2*pi", "2*pi", "2*pi", "2*pi", "2*pi", "2*pi", "2*pi", "2*pi" ], "Umin": [ "-sqrt(1.5)", "-sqrt(1.5)", "-sqrt(1.5)", "-sqrt(1.5)", "0", "0", "0", "0", "0", "0", "0", "0", "0" ], "Vmax": [ "sqrt(1.5)", "sqrt(1.5)", "sqrt(1.5)", "sqrt(1.5)", "3", "-1", "3", "-1", "3", "-1", "3", "-1", "pi/2" ], "Vmin": [ "-sqrt(1.5)", "-sqrt(1.5)", "-sqrt(1.5)", "-sqrt(1.5)", "1", "-3", "1", "-3", "1", "-3", "1", "-3", "-pi/2" ] } }, { "Param3D": { "Component": [ "HerzPolar", "Sphere" ], "Description": [ "Herz parametrized polar" ], "Fx": [ "0.5*cosh(v)*sin(u)", "cos(v)*sin(u)" ], "Fy": [ "0.5*sinh(v)*(1+cosh(v)*cos(u))", "cos(v)*cos(u)" ], "Fz": [ "0.5*(1+cosh(v)*cos(u))", "sin(v)" ], "Name": [ "Herz+Sphere1" ], "Umax": [ "2*pi", "2*pi" ], "Umin": [ "0", "0" ], "Vmax": [ "1.47", "pi/2" ], "Vmin": [ "-1.47", "-pi/2" ] } }, { "Param3D": { "Component": [ "HerzPolar", "Sphere" ], "Description": [ "Herz parametrized polar" ], "Fx": [ "0.5*cosh(v)*sin(u)", "sqrt(2)*cos(v)*sin(u)" ], "Fy": [ "0.5*sinh(v)*(1+cosh(v)*cos(u))", "sqrt(2)*cos(v)*cos(u)" ], "Fz": [ "0.5*(1+cosh(v)*cos(u))", "sqrt(2)*sin(v)" ], "Name": [ "Herz+Sphere√2" ], "Umax": [ "2*pi", "2*pi" ], "Umin": [ "0", "0" ], "Vmax": [ "1.77", "pi/2" ], "Vmin": [ "-1.77", "-pi/2" ] } }, { "Param3D": { "Component": [ "HerzPolar", "Sphere" ], "Description": [ "Herz parametrized polar" ], "Fx": [ "0.5*cosh(v)*sin(u)", "2*cos(v)*sin(u)" ], "Fy": [ "0.5*sinh(v)*(1+cosh(v)*cos(u))", "2*cos(v)*cos(u)" ], "Fz": [ "0.5*(1+cosh(v)*cos(u))", "2*sin(v)" ], "Name": [ "Herz+Sphere2" ], "Umax": [ "2*pi", "2*pi" ], "Umin": [ "0", "0" ], "Vmax": [ "2.1", "pi/2" ], "Vmin": [ "-2.1", "-pi/2" ] } }, { "Param3D": { "Component": [ "HimmerHolleP_01", "HimmerHolleP_02", "Sphere" ], "Description": [ "parametric Himmer & Hölle" ], "Fx": [ "u*v", "-u*v", "cos(v)*sin(u)" ], "Fy": [ "u", "u", "cos(v)*cos(u)" ], "Fz": [ "v", "v", "sin(v)" ], "Name": [ "Himmer & Hölle + Sphere 1" ], "Umax": [ "1", "1", "2*pi" ], "Umin": [ "-1", "-1", "0" ], "Vmax": [ "1", "1", "pi/2" ], "Vmin": [ "-1", "-1", "-pi/2" ] } }, { "Param3D": { "Component": [ "KolibriP", "Sphere" ], "Description": [ "parametrized Kolibri" ], "Fx": [ "u*(u^2-v^2)", "cos(v)*cos(u)" ], "Fy": [ "v", "cos(v)*sin(u)" ], "Fz": [ "u^2-v^2", "sin(v)" ], "Name": [ "Kolibri + Sphere 1" ], "Umax": [ "5^(1/4)/sqrt(2)", "2*pi" ], "Umin": [ "-5^(1/4)/sqrt(2)", "0" ], "Vmax": [ "5^(1/4)/sqrt(2)", "pi/2" ], "Vmin": [ "-5^(1/4)/sqrt(2)", "-pi/2" ] } }, { "Param3D": { "Component": [ "KolibriP", "Sphere" ], "Description": [ "parametrized Kolibri" ], "Fx": [ "u*(u^2-v^2)", "sqrt(2)*cos(v)*cos(u)" ], "Fy": [ "v", "sqrt(2)*cos(v)*sin(u)" ], "Fz": [ "u^2-v^2", "sqrt(2)*sin(v)" ], "Name": [ "Kolibri + Sphere √2" ], "Umax": [ "sqrt(1/2+sqrt(5/2))", "2*pi" ], "Umin": [ "-sqrt(1/2+sqrt(5/2))", "0" ], "Vmax": [ "sqrt(1/2+sqrt(5/2))", "pi/2" ], "Vmin": [ "-sqrt(1/2+sqrt(5/2))", "-pi/2" ] } }, { "Param3D": { "Component": [ "KolibriP", "Sphere" ], "Description": [ "parametrized Kolibri" ], "Fx": [ "u*(u^2-v^2)", "2*cos(v)*cos(u)" ], "Fy": [ "v", "2*cos(v)*sin(u)" ], "Fz": [ "u^2-v^2", "2*sin(v)" ], "Name": [ "Kolibri + Sphere 2" ], "Umax": [ "sqrt(1/2*(3+sqrt(26)))", "2*pi" ], "Umin": [ "-sqrt(1/2*(3+sqrt(26)))", "0" ], "Vmax": [ "sqrt(1/2*(3+sqrt(26)))", "pi/2" ], "Vmin": [ "-sqrt(1/2*(3+sqrt(26)))", "-pi/2" ] } }, { "Param3D": { "Component": [ "Kreisel_03", "Kreisel_04", "Kreisel_02", "Kreisel_01", "Kreisel_01_01" ], "Description": [ "Kreisel parametrized polar" ], "Fx": [ "sqrt(60/(1+60*(-v^3+v^2)))*cos(u)", "sqrt(60/(1+60*(v^3+v^2)))*cos(u)", "sqrt(-60*v^3/(-v^3+60*(1-v)))*cos(u)", "sqrt(60*v^3/(v^3+60*(1+v)))*cos(u)", "2*sqrt(15)*cos(v)*cos(u)" ], "Fy": [ "sqrt(60/(1+60*(-v^3+v^2)))*sin(u)", "sqrt(60/(1+60*(v^3+v^2)))*sin(u)", "sqrt(-60*v^3/(-v^3+60*(1-v)))*sin(u)", "sqrt(60*v^3/(v^3+60*(1+v)))*sin(u)", "2*sqrt(15)*cos(v)*sin(u)" ], "Fz": [ "60*sqrt(-v^3/(1+60*(v^2-v^3)))", "-60*sqrt(v^3/(1+60*(v^3+v^2)))", "-60/sqrt(-v^3+60*(1-v))", "60/sqrt(v^3+60*(1+v))", "2*sqrt(15)*sin(v)" ], "Name": [ "Kreisel⊂Sphere√60" ], "Umax": [ "2*pi", "2*pi", "2*pi", "2*pi", "2*pi" ], "Umin": [ "0", "0", "0", "0", "0" ], "Vmax": [ "0", "0.25", "0", "4", "pi/2" ], "Vmin": [ "-0.25", "0", "-4", "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "Nepali Polar", "NepaliPolar_01" ], "Description": [ "Nepali parametrized polar" ], "Fx": [ "sin(v)*cos(u)", "(2+2^(1/3))/(2*2^(2/3))*cos(v)*cos(u)" ], "Fy": [ "sin(v)*sin(u)", "(2+2^(1/3))/(2*2^(2/3))*cos(v)*sin(u)" ], "Fz": [ "-(-(sin(v)^2*sin(2*u)/2-1+cos(v)^3))^(1/3)", "(2+2^(1/3))/(2*2^(2/3))*(sin(v)-1)" ], "Name": [ "Nepali⊂Sphere" ], "Umax": [ "2*pi", "2*pi" ], "Umin": [ "0", "0" ], "Vmax": [ "pi", "pi/2" ], "Vmin": [ "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "TanzP_+", "TanzP_-", "Sphere" ], "Description": [ "parametrized Tanz" ], "Fx": [ "sqrt(1+sqrt(1+2*u^2*v^2))/2", "-sqrt(1+sqrt(1+2*u^2*v^2))/2", "sqrt(313)*cos(v)*cos(u)" ], "Fy": [ "u/sqrt(2)", "u/sqrt(2)", "sqrt(313)*cos(v)*sin(u)" ], "Fz": [ "v/sqrt(2)", "v/sqrt(2)", "sqrt(313)*sin(v)" ], "Name": [ "Tanz + Sphere √313" ], "Umax": [ "25", "25", "2*pi" ], "Umin": [ "-25", "-25", "0" ], "Vmax": [ "25", "25", "pi/2" ], "Vmin": [ "-25", "-25", "-pi/2" ] } }, { "Param3D": { "Component": [ "TaubePs_1", "TaubePs_2", "TaubePs_3", "TaubePs_4", "Sphere" ], "Description": [ "Parametric Taube" ], "Fx": [ "3*(u^2-v^2)", "-3*(u^2+v^2)", "-3*(u^2+v^2)", "3*(v^2-u^2)", "cos(v)*cos(u)" ], "Fy": [ "2*v*(3*u^2-v^2)", "-2*v*(3*u^2+v^2)", "2*u*(3*v^2+u^2)", "-2*u*(3*v^2-u^2)", "cos(v)*sin(u)" ], "Fz": [ "3*u^2*v^2", "-3*u^2*v^2", "-3*u^2*v^2", "3*u^2*v^2", "sin(v)" ], "Name": [ "Taube + Sphere 1" ], "Umax": [ "0.615", "0", "0.734145", "0.734145", "2*pi" ], "Umin": [ "0", "-0.734145", "0", "0", "0" ], "Vmax": [ "0.734145", "0.734145", "0", "0.615", "pi/2" ], "Vmin": [ "0", "0", "-0.734145", "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "TaubePs_1", "TaubePs_2", "TaubePs_3", "TaubePs_4", "Sphere" ], "Description": [ "Parametric Taube" ], "Fx": [ "3*(u^2-v^2)", "-3*(u^2+v^2)", "-3*(u^2+v^2)", "3*(v^2-u^2)", "sqrt(2)*cos(v)*cos(u)" ], "Fy": [ "2*v*(3*u^2-v^2)", "-2*v*(3*u^2+v^2)", "2*u*(3*v^2+u^2)", "-2*u*(3*v^2-u^2)", "sqrt(2)*cos(v)*sin(u)" ], "Fz": [ "3*u^2*v^2", "-3*u^2*v^2", "-3*u^2*v^2", "3*u^2*v^2", "sqrt(2)*sin(v)" ], "Name": [ "Taube + Sphere √2" ], "Umax": [ "0.692", "0", "0.84172", "0.84172", "2*pi" ], "Umin": [ "0", "-0.84172", "0", "0", "0" ], "Vmax": [ "0.84172", "0.84172", "0", "0.692", "pi/2" ], "Vmin": [ "0", "0", "-0.84172", "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "TaubePs_1", "TaubePs_2", "TaubePs_3", "TaubePs_4", "Sphere" ], "Description": [ "Parametric Taube" ], "Fx": [ "3*(u^2-v^2)", "-3*(u^2+v^2)", "-3*(u^2+v^2)", "3*(v^2-u^2)", "2*cos(v)*cos(u)" ], "Fy": [ "2*v*(3*u^2-v^2)", "-2*v*(3*u^2+v^2)", "2*u*(3*v^2+u^2)", "-2*u*(3*v^2-u^2)", "2*cos(v)*sin(u)" ], "Fz": [ "3*u^2*v^2", "-3*u^2*v^2", "-3*u^2*v^2", "3*u^2*v^2", "2*sin(v)" ], "Name": [ "Taube + Sphere 2" ], "Umax": [ "0.82", "0", "0.963985", "0.963985", "2*pi" ], "Umin": [ "0", "-0.963985", "0", "0", "0" ], "Vmax": [ "0.963985", "0.963985", "0", "0.82", "pi/2" ], "Vmin": [ "0", "0", "-0.963985", "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "TaubePs_1", "TaubePs_2", "TaubePs_3", "TaubePs_4", "Sphere" ], "Description": [ "Parametric Taube" ], "Fx": [ "3*(u^2-v^2)", "-3*(u^2+v^2)", "-3*(u^2+v^2)", "3*(v^2-u^2)", "6*cos(v)*cos(u)" ], "Fy": [ "2*v*(3*u^2-v^2)", "-2*v*(3*u^2+v^2)", "2*u*(3*v^2+u^2)", "-2*u*(3*v^2-u^2)", "6*cos(v)*sin(u)" ], "Fz": [ "3*u^2*v^2", "-3*u^2*v^2", "-3*u^2*v^2", "3*u^2*v^2", "6*sin(v)" ], "Name": [ "Taube + Sphere 6" ], "Umax": [ "1.42", "0", "1.45475", "1.45475", "2*pi" ], "Umin": [ "0", "-1.45475", "0", "0", "0" ], "Vmax": [ "1.45475", "1.45475", "0", "1.42", "pi/2" ], "Vmin": [ "0", "0", "-1.45475", "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "TaubePs_1", "TaubePs_2", "TaubePs_3", "TaubePs_4", "Sphere" ], "Description": [ "Parametric Taube" ], "Fx": [ "3*(u^2-v^2)", "-3*(u^2+v^2)", "-3*(u^2+v^2)", "3*(v^2-u^2)", "12*cos(v)*cos(u)" ], "Fy": [ "2*v*(3*u^2-v^2)", "-2*v*(3*u^2+v^2)", "2*u*(3*v^2+u^2)", "-2*u*(3*v^2-u^2)", "12*cos(v)*sin(u)" ], "Fz": [ "3*u^2*v^2", "-3*u^2*v^2", "-3*u^2*v^2", "3*u^2*v^2", "12*sin(v)" ], "Name": [ "Taube + Sphere 12" ], "Umax": [ "2", "0", "1.85398", "1.85398", "2*pi" ], "Umin": [ "0", "-2", "0", "0", "0" ], "Vmax": [ "1.85398", "1.85398", "0", "2", "pi/2" ], "Vmin": [ "0", "0", "-2", "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "TulleP_01", "TulleP_02", "TulleP_03", "Sphere" ], "Description": [ "parametrized Tulle" ], "Fx": [ "v", "u", "u", "cos(v)*cos(u)" ], "Fy": [ "0.5*(u-v^2)", "0", "v", "cos(v)*sin(u)" ], "Fz": [ "0.5*(u+v^2)", "v", "0", "sin(v)" ], "Name": [ "Tulle + Sphere 1" ], "Umax": [ "sqrt(2)", "1", "1", "2*pi" ], "Umin": [ "-sqrt(2)", "-1", "-1", "0" ], "Vmax": [ "1", "1", "1", "pi/2" ], "Vmin": [ "-1", "-1", "-1", "-pi/2" ] } }, { "Param3D": { "Component": [ "TulleP_01", "TulleP_02", "TulleP_03", "Sphere" ], "Description": [ "parametrized Tulle" ], "Fx": [ "v", "u", "u", "sqrt(2)*cos(v)*cos(u)" ], "Fy": [ "0.5*(u-v^2)", "0", "v", "sqrt(2)*cos(v)*sin(u)" ], "Fz": [ "0.5*(u+v^2)", "v", "0", "sqrt(2)*sin(v)" ], "Name": [ "Tulle + Sphere √2" ], "Umax": [ "2", "sqrt(2)", "sqrt(2)", "2*pi" ], "Umin": [ "-2", "-sqrt(2)", "-sqrt(2)", "0" ], "Vmax": [ "sqrt(2)", "sqrt(2)", "sqrt(2)", "pi/2" ], "Vmin": [ "-sqrt(2)", "-sqrt(2)", "-sqrt(2)", "-pi/2" ] } }, { "Param3D": { "Component": [ "TulleP_01", "TulleP_02", "TulleP_03", "Sphere" ], "Description": [ "parametrized Tulle" ], "Fx": [ "v", "u", "u", "2*cos(v)*cos(u)" ], "Fy": [ "0.5*(u-v^2)", "0", "v", "2*cos(v)*sin(u)" ], "Fz": [ "0.5*(u+v^2)", "v", "0", "2*sin(v)" ], "Name": [ "Tulle + Sphere 2" ], "Umax": [ "2*sqrt(2)", "2", "2", "2*pi" ], "Umin": [ "-2*sqrt(2)", "-2", "-2", "0" ], "Vmax": [ "2", "2", "2", "pi/2" ], "Vmin": [ "-2", "-2", "-2", "-pi/2" ] } }, { "Param3D": { "Component": [ "Zeek Polar", "Sphere" ], "Description": [ "Parametric Zeek" ], "Fx": [ "sin(v)*cos(v)^3*cos(u)", "cos(v)*cos(u)/2" ], "Fy": [ "sin(v)*cos(v)^3*sin(u)", "cos(v)*sin(u)/2" ], "Fz": [ "cos(v)^2", "(sin(v)+1)/2" ], "Name": [ "Zeek⊂Sphere½" ], "Umax": [ "2*pi", "2*pi" ], "Umin": [ "0", "0" ], "Vmax": [ "pi/2", "pi/2" ], "Vmin": [ "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "SpitzPolar_+", "SpitzPolar_-", "Sphere" ], "Description": [ "Parametric Spitz" ], "Fx": [ "4*v^3*cos(u)", "4*v^3*cos(u)", "cos(v)*cos(u)" ], "Fy": [ "6*v^2*(sin(2*u)^2)^(1/3)+sqrt(4*v^2*(sin(2*u)^4)^(1/3)+16*v^6)", "6*v^2*(sin(2*u)^2)^(1/3)-sqrt(4*v^2*(sin(2*u)^4)^(1/3)+16*v^6)", "cos(v)*sin(u)" ], "Fz": [ "4*v^3*sin(u)", "4*v^3*sin(u)", "sin(v)" ], "Name": [ "Spitz +Sphere 1" ], "Umax": [ "2*pi", "2*pi", "2*pi" ], "Umin": [ "0", "0", "0" ], "Vmax": [ "1/2^(5/6)", "0.63", "pi/2" ], "Vmin": [ "0", "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "SpitzPolar_+", "SpitzPolar_-", "Sphere" ], "Description": [ "Parametric Spitz" ], "Fx": [ "4*v^3*cos(u)", "4*v^3*cos(u)", "sqrt(2)*cos(v)*cos(u)" ], "Fy": [ "6*v^2*(sin(2*u)^2)^(1/3)+sqrt(4*v^2*(sin(2*u)^4)^(1/3)+16*v^6)", "6*v^2*(sin(2*u)^2)^(1/3)-sqrt(4*v^2*(sin(2*u)^4)^(1/3)+16*v^6)", "sqrt(2)*cos(v)*sin(u)" ], "Fz": [ "4*v^3*sin(u)", "4*v^3*sin(u)", "sqrt(2)*sin(v)" ], "Name": [ "Spitz +Sphere √2" ], "Umax": [ "2*pi", "2*pi", "2*pi" ], "Umin": [ "0", "0", "0" ], "Vmax": [ "1/2^(2/3)", "0.71", "pi/2" ], "Vmin": [ "0", "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "SpitzPolar_+", "SpitzPolar_-", "Sphere" ], "Description": [ "Parametric Spitz" ], "Fx": [ "4*v^3*cos(u)", "4*v^3*cos(u)", "2*cos(v)*cos(u)" ], "Fy": [ "6*v^2*(sin(2*u)^2)^(1/3)+sqrt(4*v^2*(sin(2*u)^4)^(1/3)+16*v^6)", "6*v^2*(sin(2*u)^2)^(1/3)-sqrt(4*v^2*(sin(2*u)^4)^(1/3)+16*v^6)", "2*cos(v)*sin(u)" ], "Fz": [ "4*v^3*sin(u)", "4*v^3*sin(u)", "2*sin(v)" ], "Name": [ "Spitz +Sphere 2" ], "Umax": [ "2*pi", "2*pi", "2*pi" ], "Umin": [ "0", "0", "0" ], "Vmax": [ "1/sqrt(2)", "0.8", "pi/2" ], "Vmin": [ "0", "0", "-pi/2" ] } }, { "Param3D": { "Component": [ "SchneeflockePX_1", "SchneeflockePX_2", "SchneeflockePX_3", "SchneeflockePX_4", "Sphere" ], "Description": [ "Parametric Schneeflocke" ], "Fx": [ "(u-v)*(u*v)^(1/3)", "-(u-v)*(-u*v)^(1/3)", "(u-v)*(u*v)^(1/3)", "-(u-v)*(-u*v)^(1/3)", "cos(v)*cos(u)" ], "Fy": [ "u", "u", "u", "u", "cos(v)*sin(u)" ], "Fz": [ "v-u", "v-u", "v-u", "v-u", "sin(v)" ], "Name": [ "Schneeflocke +Sphere 1" ], "Umax": [ "1", "0", "0", "1", "2*pi" ], "Umin": [ "0", "-1", "-1", "0", "0" ], "Vmax": [ "1.23", "1.23", "0", "0", "pi/2" ], "Vmin": [ "0", "0", "-1.23", "-1.23", "-pi/2" ] } }, { "Param3D": { "Component": [ "SchneeflockePX_1", "SchneeflockePX_2", "SchneeflockePX_3", "SchneeflockePX_4", "Sphere" ], "Description": [ "Parametric Schneeflocke" ], "Fx": [ "(u-v)*(u*v)^(1/3)", "-(u-v)*(-u*v)^(1/3)", "(u-v)*(u*v)^(1/3)", "-(u-v)*(-u*v)^(1/3)", "sqrt(2)*cos(v)*cos(u)" ], "Fy": [ "u", "u", "u", "u", "sqrt(2)*cos(v)*sin(u)" ], "Fz": [ "v-u", "v-u", "v-u", "v-u", "sqrt(2)*sin(v)" ], "Name": [ "Schneeflocke +Sphere √2" ], "Umax": [ "sqrt(2)", "0", "0", "sqrt(2)", "2*pi" ], "Umin": [ "0", "-sqrt(2)", "-sqrt(2)", "0", "0" ], "Vmax": [ "1.67", "1.67", "0", "0", "pi/2" ], "Vmin": [ "0", "0", "-1.67", "-1.67", "-pi/2" ] } }, { "Param3D": { "Component": [ "SchneeflockePX_1", "SchneeflockePX_2", "SchneeflockePX_3", "SchneeflockePX_4", "Sphere" ], "Description": [ "Parametric Schneeflocke" ], "Fx": [ "(u-v)*(u*v)^(1/3)", "-(u-v)*(-u*v)^(1/3)", "(u-v)*(u*v)^(1/3)", "-(u-v)*(-u*v)^(1/3)", "2*cos(v)*cos(u)" ], "Fy": [ "u", "u", "u", "u", "2*cos(v)*sin(u)" ], "Fz": [ "v-u", "v-u", "v-u", "v-u", "2*sin(v)" ], "Name": [ "Schneeflocke +Sphere 2" ], "Umax": [ "2", "0", "0", "2", "2*pi" ], "Umin": [ "0", "-2", "-2", "0", "0" ], "Vmax": [ "2.27", "2.27", "0", "0", "pi/2" ], "Vmin": [ "0", "0", "-2.27", "-2.27", "-pi/2" ] } } ] }
Voyons comment construire un modèle à partir de sa formule en utilisant l'exemple de Kolibri.
Image de Kolibri dans la galérie Herwig Hauser Classic:

L'équation de Kolibri, x2=y2z2+z3, est une équation implicite.
Le logiciel MathMod peut lui faire directement un maillage, mais il ne sera pas forcement très propre. (Apparemment ce logiciel a du mal à gérer les courbes et points singuliers :
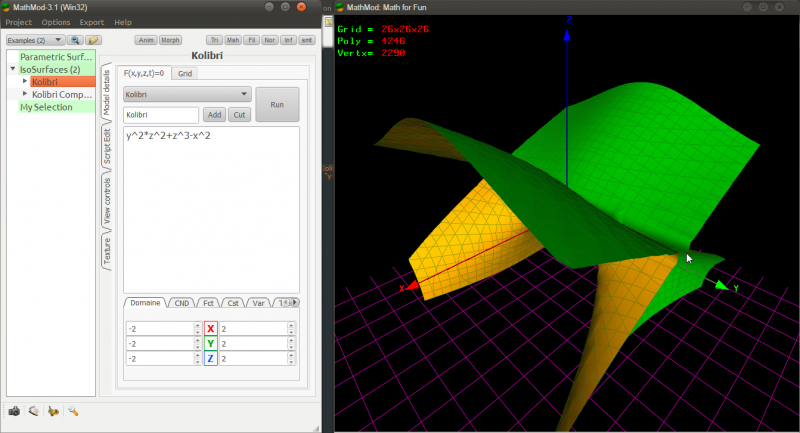 Une façon de contourner ce problème est de casser le modèle en morceaux, ce qui peut-être suffisant pour avoir un rendu intéressant sur l'écran, mais n'est souvent pas suffisant pour avoir un beau modèle 3D autour d'un point singulier de la surface:
Une façon de contourner ce problème est de casser le modèle en morceaux, ce qui peut-être suffisant pour avoir un rendu intéressant sur l'écran, mais n'est souvent pas suffisant pour avoir un beau modèle 3D autour d'un point singulier de la surface:
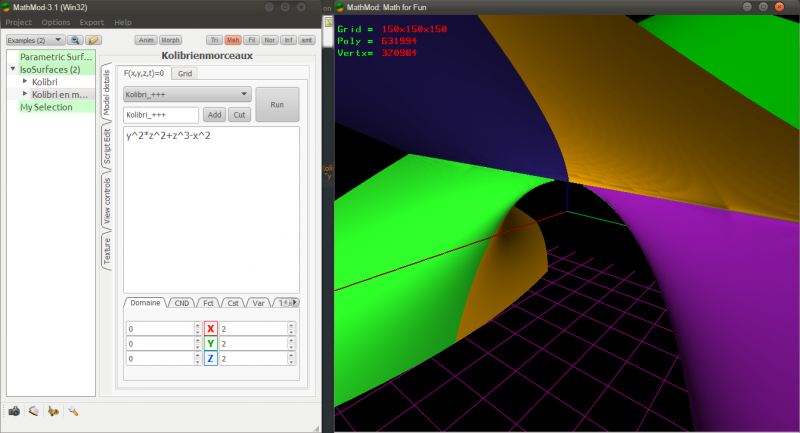 On préférera donc passer par une forme paramétrée de Kolibri. Pour cela on fait la substitution x = u z. Après cette substitution l'équation devient u2z2=y2z2+z3 qu'on peut simplifier en
On préférera donc passer par une forme paramétrée de Kolibri. Pour cela on fait la substitution x = u z. Après cette substitution l'équation devient u2z2=y2z2+z3 qu'on peut simplifier en
$u^2=y^2+z$
u2=y2+z
pour tout z≠0. En posant y=v, on obtient donc la paramétrisation suivante de Kolibri:
x=u (u2 − v2)
y=v
z=u2 − v2
C'est une parametrisation globale, c'est à dire que tous les points de la surfaces sont décrits par cette paramétrisation.
On peut visualiser le résultat pour −1≤u≤1 et −1≤v≤1 sur MathMod et l'exporter au format *.obj.
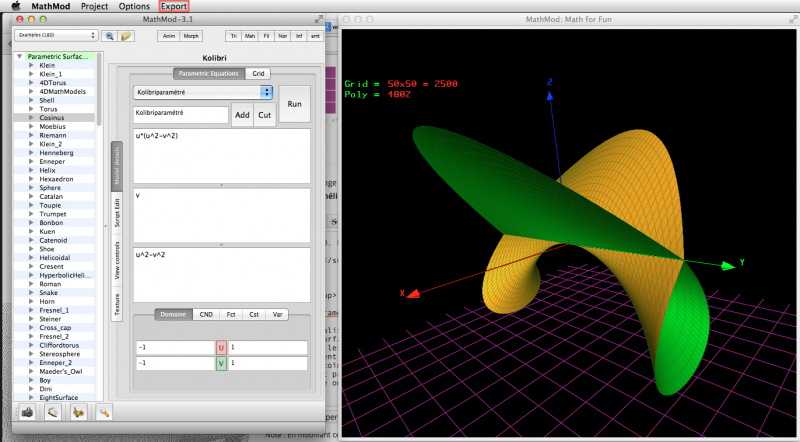 En pratique, les objets de la galérie de Herwig Hauser sont intersectés avec des sphères ou des cubes. L'image de Kolibri est visiblement intersectée avec une sphère. Comme MathMod pose le centre de référentiel au centre géométrique de l'objet, celui-ci ne coïncide pas toujours avec l'origine du référentiel ayant donné lieu à l'équation. (Pour Kolibri il conïncide! mais ce n'est pas le cas le plus commun). Donc, si on veut intersecter la surface avec une sphère, on mettra la sphère avec laquelle on intersecte avant d'exporter l'objet. Dans MathMod cela revient à rajouter une composante sphérique à l'objet :
En pratique, les objets de la galérie de Herwig Hauser sont intersectés avec des sphères ou des cubes. L'image de Kolibri est visiblement intersectée avec une sphère. Comme MathMod pose le centre de référentiel au centre géométrique de l'objet, celui-ci ne coïncide pas toujours avec l'origine du référentiel ayant donné lieu à l'équation. (Pour Kolibri il conïncide! mais ce n'est pas le cas le plus commun). Donc, si on veut intersecter la surface avec une sphère, on mettra la sphère avec laquelle on intersecte avant d'exporter l'objet. Dans MathMod cela revient à rajouter une composante sphérique à l'objet :
Après avoir exporté le fichier au format *.obj depuis MathMod, on importe le résultat dans Blender (on fera attention à demarrer avec un fichier Blender sans autre objet3D, en particulier on éliminera le cube qui apparaît par défaut dans tout nouveau fichier. La touche pour éliminer c'est X.):
Vous pouvez appuyer sur la touche “point” (ou “virgule”) du clavier numérique pour vous retrouver avec une vue centrée sur votre objet :
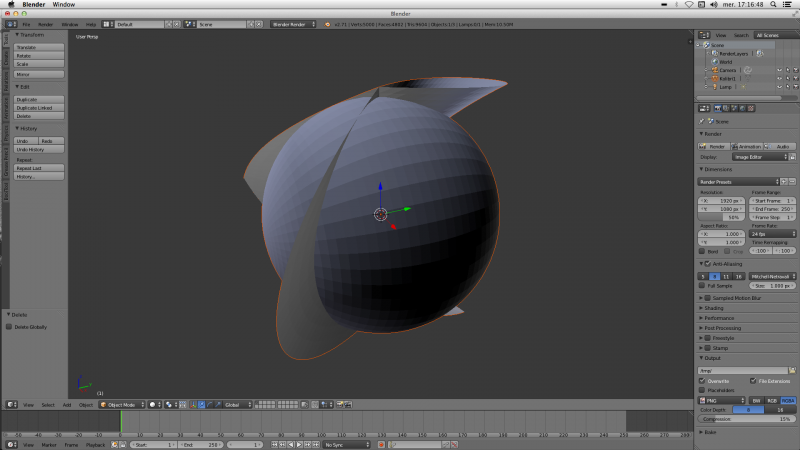 Vous remarquerez que sur cette image les facettes sont visibles. C'est parce que nous avons utilisé une résolution de la paramétrisation assez basse (50×50). Celle-ci est cependant suffisante pour des petites impressions, rappelez-vous que la résolution de l'imprimante ne va pas en dessous d'un micron.
Vous remarquerez que sur cette image les facettes sont visibles. C'est parce que nous avons utilisé une résolution de la paramétrisation assez basse (50×50). Celle-ci est cependant suffisante pour des petites impressions, rappelez-vous que la résolution de l'imprimante ne va pas en dessous d'un micron.
L'objet importé est énorme. Dans ce qui suit, nous supposerons que Blender est en unités métriques. (Les unités que Blender considère se trouvent dans le menu Scène). Pour mettre à l'échelle, appuyez sur la touche S puis tapez le facteur d'échelle au clavier numérique et enfin appuyez sur Enter. Pour calculer le bon facteur d'échelle, vous pouvez sélectionner deux sommets de la figure (dans le mode édition de Blender), calculer leur distance et calculer le facteur necessaire pour ramener cette distance à la distance souhaitée entre ces deux points.
Concrètement, supposons que nous voulons mettre Kolibri dans une sphère de rayon 2.8cm (le but étant de le présenter ensuite dans une boule en plexiglas de diamètre 6cm). Appuyez sur la touche 1 du clavier numérique pour nous mettre en vue de face. Appuyez sur “Tab” pour changer en mode édition. Faites clic droit un sommet central de la sphère en face de vous. Appuyez sur la touche N pour voir les informations sur les sommets selectionnés :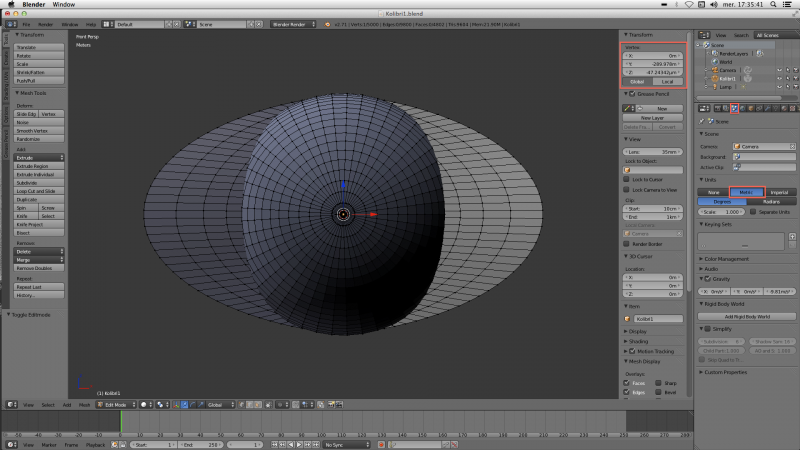 On y voit que les coordonnées de ce sommets sont
On y voit que les coordonnées de ce sommets sont
x = 0m
y = −289.978m
z = −47.24342μm
Pour le sommet opposé, on appuie sur la combinaison de touches Ctrl+1 pour avoir la vue de dos et on choisi de nouveau le sommet au centre de la sphère. On obtient les coordonnées suivantes:
x = 0m
y = 289.978m
z = 47.24342μm
La distance entre ces deux sommets est le diamètre de la sphère. Dans notre exemple, le diamètre vaut donc : 579.956m. Le rayon vaut 289.978m, mais nous voulons un rayons de 0.028. Notre facteur d'échelle est donc 0.0000965590… Repassez en mode objet avec la touche “Tab”, appuyez sur la touche S, puis tapez 0.000096559 au clavier numérique, et sur la touche “point/virgule” du clavier numérique pour zoomer sur votre objet:
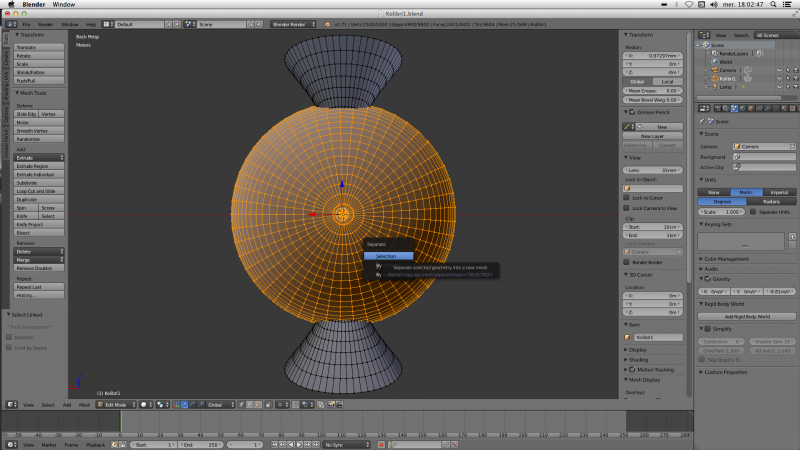
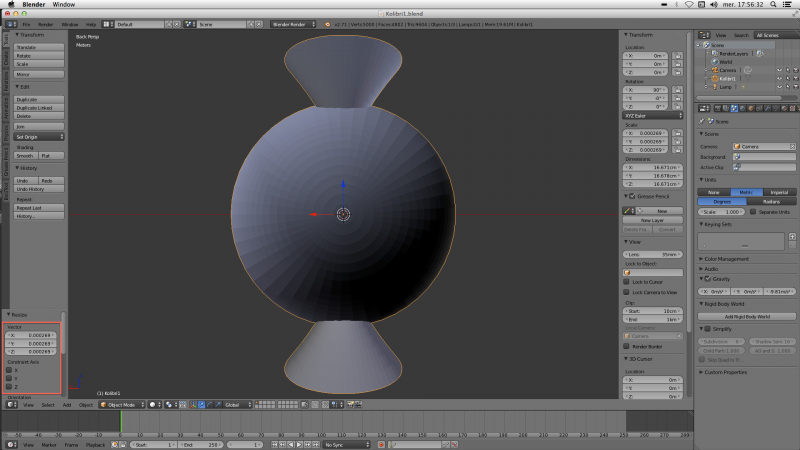 A continuation, on sépare la sphère du reste de l'objet. Pour cela, on repasse en mode d'édition avec la touche “Tab”, et on selectionne (clic droit) n'importe quel sommet de la sphère. Avec la touche L on choisi tous les autres sommets de la sphère. Avec la touche W, on va dans un menu ou on choisi l'option “remove doubles” pour que notre sphere devienne une surface fermée (c'est necessaire pour faire des interesections). On appuie ensuite sur la touche P qui permet de séparer un objet en 2 et on fait le choix de séparer les sommets selectionnés, c'est-à-dire la sphère :
A continuation, on sépare la sphère du reste de l'objet. Pour cela, on repasse en mode d'édition avec la touche “Tab”, et on selectionne (clic droit) n'importe quel sommet de la sphère. Avec la touche L on choisi tous les autres sommets de la sphère. Avec la touche W, on va dans un menu ou on choisi l'option “remove doubles” pour que notre sphere devienne une surface fermée (c'est necessaire pour faire des interesections). On appuie ensuite sur la touche P qui permet de séparer un objet en 2 et on fait le choix de séparer les sommets selectionnés, c'est-à-dire la sphère :
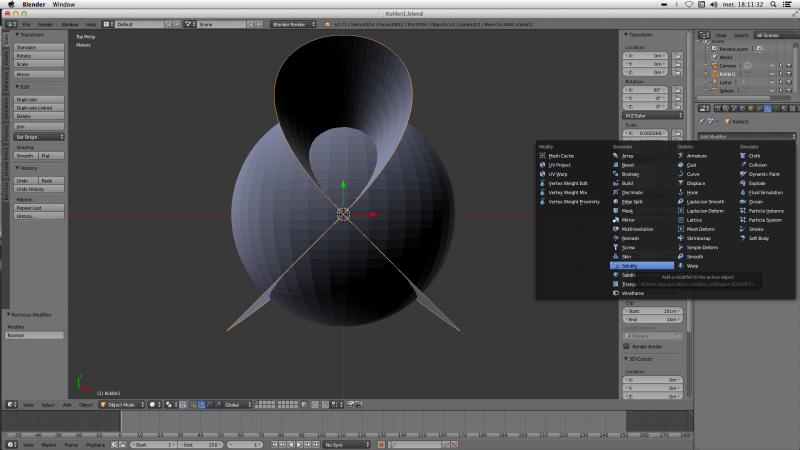
 On appuie sur la touche “Tab” pour repasser en mode objet. Pour ne pas s'embrouiller, on change le nom de la sphere. (On peut l'appeler “sphere”, ça se passe en haut à droite). On choisit aussi temporairement de ne pas visualiser la sphere pour ne pas s'emmêler les pinceaux. On selectionne la surface Kolibri (clic droit) et on lui applique le modificateur “solidify” pour lui donner de l'épaisseur :
On appuie sur la touche “Tab” pour repasser en mode objet. Pour ne pas s'embrouiller, on change le nom de la sphere. (On peut l'appeler “sphere”, ça se passe en haut à droite). On choisit aussi temporairement de ne pas visualiser la sphere pour ne pas s'emmêler les pinceaux. On selectionne la surface Kolibri (clic droit) et on lui applique le modificateur “solidify” pour lui donner de l'épaisseur :
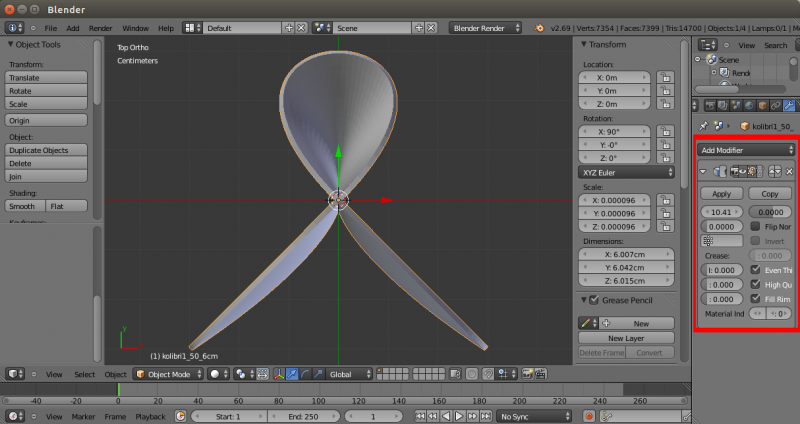
 Dans les paramètres de solidify, on pose Offset=0 et on active les options “Even Thickness” et “High Quality” pour un résultat plus uniforme. Plus le paramètre Thickness est grand, plus l'épaisseur est grande, mais Thickness ne vaut pas exactement l'épaisseur. L'idée c'est d'avoir une épaisseur à la fin d'au moins 1mm à l'impression (en déça, la machine n'y arrivera pas) mais pas beacoup plus grande que 2mm (sinon, l'impression prend beaucoup de temps). Par essais et erreur, on voit que pour une valeur Thickness=10.41, on obtient une épaisseur d'un 1mm :
Dans les paramètres de solidify, on pose Offset=0 et on active les options “Even Thickness” et “High Quality” pour un résultat plus uniforme. Plus le paramètre Thickness est grand, plus l'épaisseur est grande, mais Thickness ne vaut pas exactement l'épaisseur. L'idée c'est d'avoir une épaisseur à la fin d'au moins 1mm à l'impression (en déça, la machine n'y arrivera pas) mais pas beacoup plus grande que 2mm (sinon, l'impression prend beaucoup de temps). Par essais et erreur, on voit que pour une valeur Thickness=10.41, on obtient une épaisseur d'un 1mm :
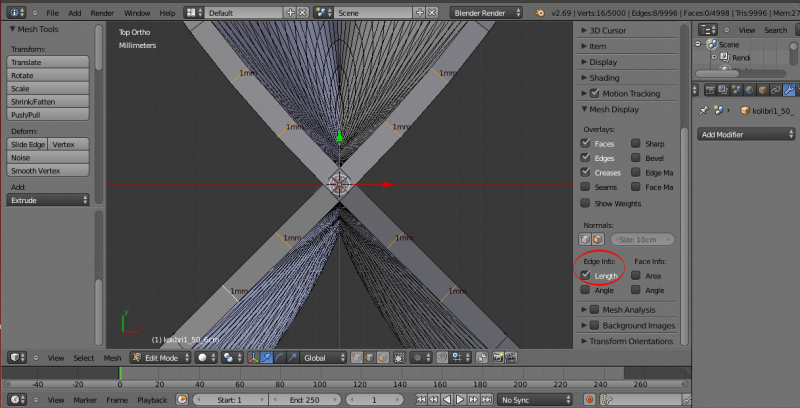
 Pour vérifier l'épaisseur, après avoir solidifié la surface, on choisi une arête du bord et dans les options de visualisation on coche la case “Length” du champ “Edge Info” dans les options de visualisation :
Pour vérifier l'épaisseur, après avoir solidifié la surface, on choisi une arête du bord et dans les options de visualisation on coche la case “Length” du champ “Edge Info” dans les options de visualisation :
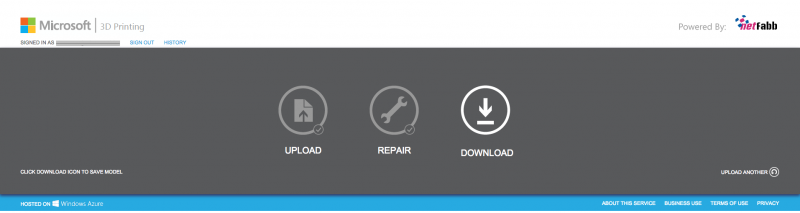
 En ce moment, la surface possède des auto-intersections. Les autointersections sont embêtantes au moment de l'impression, car les espaces couverts deux fois peuvent être considérés comme des espaces vides. Pour nettoyer les auto-intersections, on utilisera un utilitaire en ligne, Netfabb sur le serveur Windows Azure (un compte Microsoft est necessaire pour pouvoir l'utiliser). En voici le lien: modelrepair.azurewebsites.net. On exporte donc de Blender au format stl, on uploade sur Netfabb, on attend quelques instants et on télécharge le fichier stl corrigé lequel on reimporte dans Blender:
En ce moment, la surface possède des auto-intersections. Les autointersections sont embêtantes au moment de l'impression, car les espaces couverts deux fois peuvent être considérés comme des espaces vides. Pour nettoyer les auto-intersections, on utilisera un utilitaire en ligne, Netfabb sur le serveur Windows Azure (un compte Microsoft est necessaire pour pouvoir l'utiliser). En voici le lien: modelrepair.azurewebsites.net. On exporte donc de Blender au format stl, on uploade sur Netfabb, on attend quelques instants et on télécharge le fichier stl corrigé lequel on reimporte dans Blender:
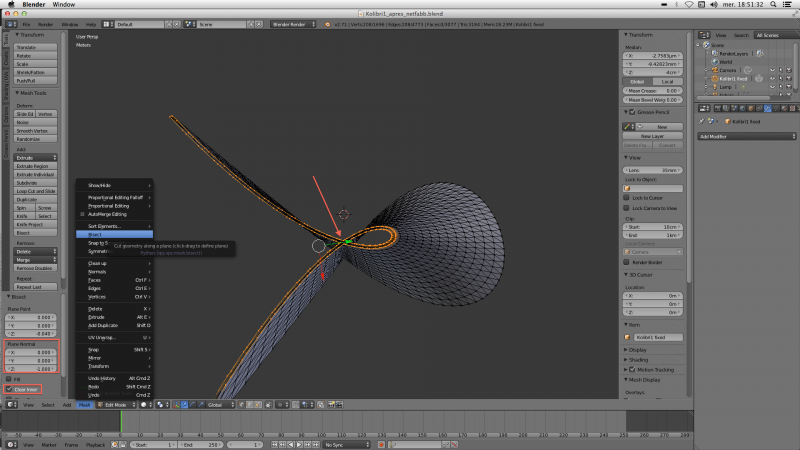
On peut vérifier qu'il n'y a plus d'auto-intersection avec l'outil “bissect” disponible en mode édition:
 On est maintenant prêts pour intersecter avec la sphère. On utilise pour cela le modifier “Boolean”:
On est maintenant prêts pour intersecter avec la sphère. On utilise pour cela le modifier “Boolean”:
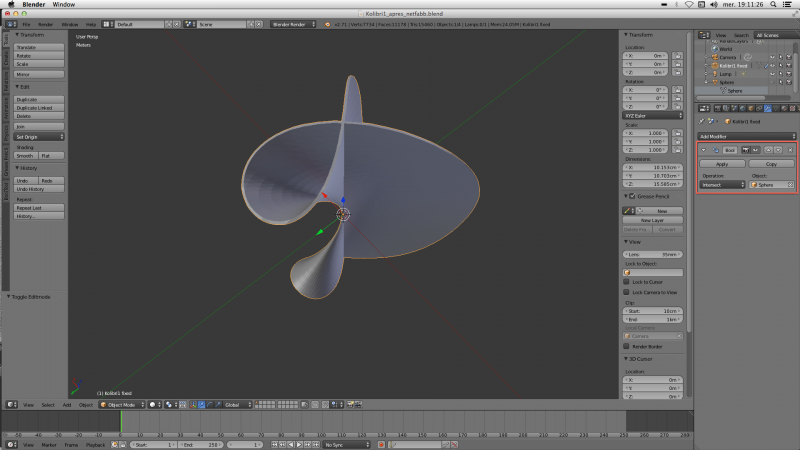
On reprend le modèle kolibri1_50_6cm_fixed_intersected.stl . Avant de l'imprimer, il faut le passer par un “slicer”, c'est-à-dire un logiciel qui calculera le parcours de la tête de l'imprimante 3D tranche par tranche. Au LFO il y a plus d'une imprimante 3D, mais pour ce projet la seule à avoir été utilisée c'est l'Ultimaker2/ Le slicer associé à l'Ultimaker 2, c'est Cura, il est disponible sur les machines du LFO.
On commence donc par importer le fichier stl dans Cura :
 Dans Cura, on selectionne l'objet avec un clic gauche, on clic sur échelle, et on vérifie que les valeurs nous conviennent et que l'objet a l'air correct :
Dans Cura, on selectionne l'objet avec un clic gauche, on clic sur échelle, et on vérifie que les valeurs nous conviennent et que l'objet a l'air correct :
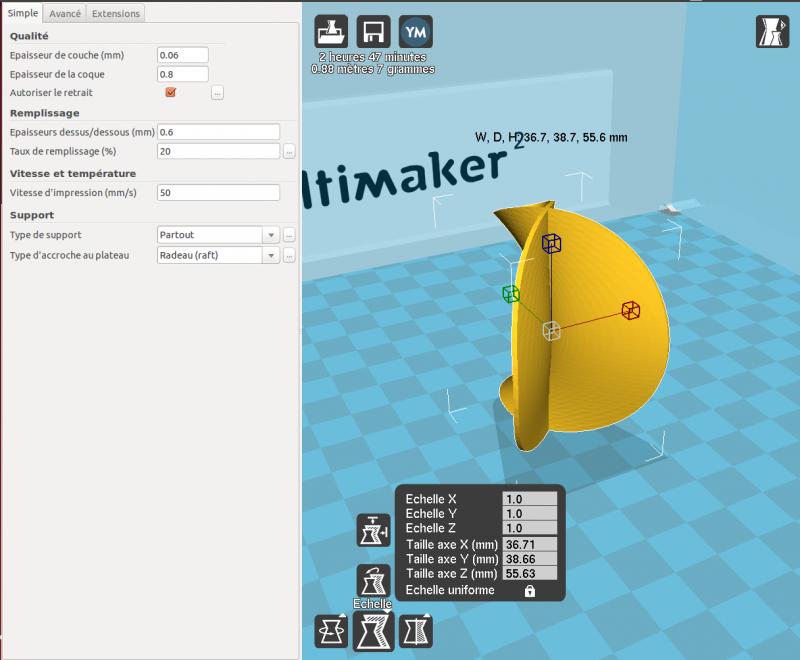 Par exemple ici, on voit que les dimensions correspondent bien, par contre le modèle a l'air d'avoir quelques stries. Par rapport à la taille à laquelle on veut l'imprimer, ça peut-être ou pas dérangeant, mais ça dépend du goût de chacun. En tout cas, pour la suite du tutoriel on décide de parier que c'est suffisant.
Par exemple ici, on voit que les dimensions correspondent bien, par contre le modèle a l'air d'avoir quelques stries. Par rapport à la taille à laquelle on veut l'imprimer, ça peut-être ou pas dérangeant, mais ça dépend du goût de chacun. En tout cas, pour la suite du tutoriel on décide de parier que c'est suffisant.
Le prochain pas est d'éventuellement tourner l'objet pour avoir moins de pentes trop aplaties. Ici, on tourne de 90° pour avoir la tête du colibri vers le haut :
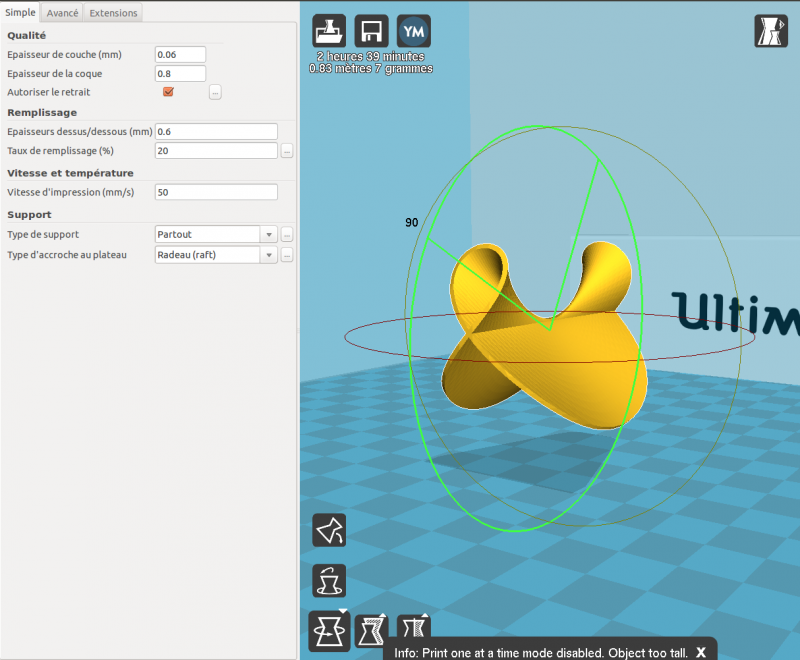
On vérifie qu'il y a assez de supports (la valeur par défaut de l'angle minimal pour les supports dans Cura est de 60°, mais cette valeur est souvent insuffisante dans l'impression de surfaces mathématiques). On peut visualiser les supports dans le mode de visualisation par couches de Cura.
On exporte alors le gcode et on sauvegarde le profil pour réutiliser la même configuration si celle-ci a du succès:
Autres photos, galerie, …